Arjun Suresh (talk | contribs) |
Arjun Suresh (talk | contribs) |
||
| Line 1: | Line 1: | ||
| − | '''1.''' If <math>L</math> and <math>L'</math> are both recursively enumerable, then <math>L</math> is recursive. Why? | + | =='''1.''' If <math>L</math> and <math>L'</math> are both recursively enumerable, then <math>L</math> is recursive. Why?== |
==={{Template:Author|Arjun Suresh|{{arjunweb}} }}=== | ==={{Template:Author|Arjun Suresh|{{arjunweb}} }}=== | ||
| Line 8: | Line 8: | ||
So, if a word is given (either from <math>L</math> or not from <math>L</math>), give it to both those $TM$s. If its from $L$, the first $TM$ will halt and we say it belongs to $L$. If its not from $L$, the second one will halt and we say it doesn't belong to <math>L</math>. Thus, <math>L</math> becomes recursive. | So, if a word is given (either from <math>L</math> or not from <math>L</math>), give it to both those $TM$s. If its from $L$, the first $TM$ will halt and we say it belongs to $L$. If its not from $L$, the second one will halt and we say it doesn't belong to <math>L</math>. Thus, <math>L</math> becomes recursive. | ||
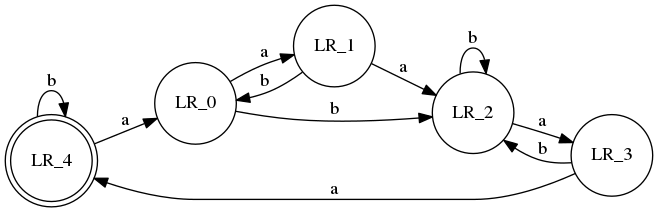
| + | =='''2.''' CYCLE(L) ={xy | yx is in L ,L is regular } == | ||
| + | Is this statement true or false ? | ||
| + | ==={{Template:Author|Arjun Suresh|{{arjunweb}} }}=== | ||
| + | We have a DFA for L, let it be D and have n states. Now we can make a NFA for L' as follows: | ||
| + | For every state of D, | ||
| + | <graphviz> | ||
| + | digraph finite_state_machine { | ||
| + | rankdir=LR; | ||
| + | size="8,5" | ||
| + | node [shape = doublecircle]; LR_0 LR_3 LR_4 LR_8; | ||
| + | node [shape = circle]; | ||
| + | LR_0 -> LR_2 [ label = "SS(B)" ]; | ||
| + | LR_0 -> LR_1 [ label = "SS(S)" ]; | ||
| + | LR_1 -> LR_3 [ label = "S($end)" ]; | ||
| + | LR_2 -> LR_6 [ label = "SS(b)" ]; | ||
| + | LR_2 -> LR_5 [ label = "SS(a)" ]; | ||
| + | LR_2 -> LR_4 [ label = "S(A)" ]; | ||
| + | LR_5 -> LR_7 [ label = "S(b)" ]; | ||
| + | LR_5 -> LR_5 [ label = "S(a)" ]; | ||
| + | LR_6 -> LR_6 [ label = "S(b)" ]; | ||
| + | LR_6 -> LR_5 [ label = "S(a)" ]; | ||
| + | LR_7 -> LR_8 [ label = "S(b)" ]; | ||
| + | LR_7 -> LR_5 [ label = "S(a)" ]; | ||
| + | LR_8 -> LR_6 [ label = "S(b)" ]; | ||
| + | LR_8 -> LR_5 [ label = "S(a)" ]; | ||
| + | } | ||
| + | </graphviz> | ||
{{Template:FBD}} | {{Template:FBD}} | ||
Given <math>L</math> is $RE$. So there is a $TM$, which accepts and halts for all words in <math>L</math>. Now, if <math>L'</math> is $RE$, then there is a $TM$, which accepts and halts for all words not in <math>L</math>. So, if a word is given (either from <math>L</math> or not from <math>L</math>), give it to both those $TM$s. If its from $L$, the first $TM$ will halt and we say it belongs to $L$. If its not from $L$, the second one will halt and we say it doesn't belong to <math>L</math>. Thus, <math>L</math> becomes recursive.
Is this statement true or false ?
We have a DFA for L, let it be D and have n states. Now we can make a NFA for L' as follows:
For every state of D,
1. If <math>L</math> and <math>L'</math> are both recursively enumerable, then <math>L</math> is recursive. Why?
Given <math>L</math> is $RE$. So there is a $TM$, which accepts and halts for all words in <math>L</math>. Now, if <math>L'</math> is $RE$, then there is a $TM$, which accepts and halts for all words not in <math>L</math>. So, if a word is given (either from <math>L</math> or not from <math>L</math>), give it to both those $TM$s. If its from $L$, the first $TM$ will halt and we say it belongs to $L$. If its not from $L$, the second one will halt and we say it doesn't belong to <math>L</math>. Thus, <math>L</math> becomes recursive.