Arjun Suresh (talk | contribs) |
Arjun Suresh (talk | contribs) |
||
| (6 intermediate revisions by the same user not shown) | |||
| Line 6: | Line 6: | ||
*'''Q:''' After converting from NFA to DFA and we get $2^n$ states. Now we apply minimization- how many states can we get after this? | *'''Q:''' After converting from NFA to DFA and we get $2^n$ states. Now we apply minimization- how many states can we get after this? | ||
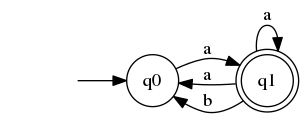
| − | In the worst case this can remain $2^n$ - that is no minimization can be possible. We can see this in the following example | + | A: In the worst case this can remain $2^n$ - that is no minimization can be possible. We can see this in the following example |
| − | + | ===NFA=== | |
<graphviz caption='NFA'> | <graphviz caption='NFA'> | ||
digraph NFA { | digraph NFA { | ||
rankdir=LR; | rankdir=LR; | ||
node [shape = none] ""; | node [shape = none] ""; | ||
| − | node [shape = doublecircle] | + | node [shape = doublecircle] q2; |
node [shape = circle]; | node [shape = circle]; | ||
| − | "" | + | ""-> q1; |
| − | |||
| − | |||
q1->q1 [label="a"]; | q1->q1 [label="a"]; | ||
| − | q1 -> | + | q1->q2 [label="a"]; |
| + | q2 -> q2 [label="b"]; | ||
} | } | ||
</graphviz> | </graphviz> | ||
| + | |||
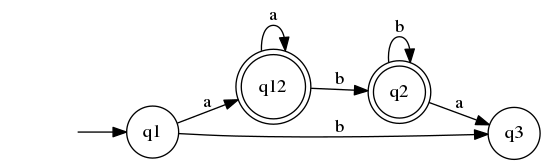
| + | ===DFA=== | ||
<graphviz caption='DFA'> | <graphviz caption='DFA'> | ||
digraph DFA { | digraph DFA { | ||
rankdir=LR; | rankdir=LR; | ||
node [shape = none] ""; | node [shape = none] ""; | ||
| − | node [shape = doublecircle] | + | node [shape = doublecircle] q2, q12; |
node [shape = circle]; | node [shape = circle]; | ||
| − | ""-> | + | ""-> q1; |
| − | + | q1->q12 [label="a"]; | |
| − | + | q12->q12 [label="a"]; | |
| − | + | q12->q2 [label="b"]; | |
| − | q1 -> | + | q2->q2 [label="b"]; |
| + | q2 -> q3 [label="a"]; | ||
| + | q1 -> q3 [label="b"]; | ||
} | } | ||
</graphviz> | </graphviz> | ||
A: I would say 1 because the $n$ states can be connected through $ε$ moves and hence all of these will be combines to a single start state in DFA.
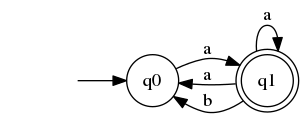
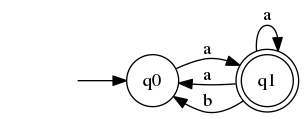
A: In the worst case this can remain $2^n$ - that is no minimization can be possible. We can see this in the following example
A: I would say 1 because the $n$ states can be connected through $ε$ moves and hence all of these will be combines to a single start state in DFA.
In the worst case this can remain $2^n$ - that is no minimization can be possible. We can see this in the following example