Arjun Suresh (talk | contribs) |
Arjun Suresh (talk | contribs) |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 6: | Line 6: | ||
*'''Q:''' After converting from NFA to DFA and we get $2^n$ states. Now we apply minimization- how many states can we get after this? | *'''Q:''' After converting from NFA to DFA and we get $2^n$ states. Now we apply minimization- how many states can we get after this? | ||
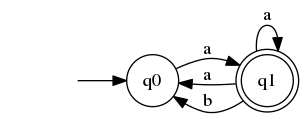
| − | In the worst case this can remain $2^n$ - that is no minimization can be possible. We can see this in the following example | + | A: In the worst case this can remain $2^n$ - that is no minimization can be possible. We can see this in the following example |
| − | + | ===NFA=== | |
<graphviz caption='NFA'> | <graphviz caption='NFA'> | ||
digraph NFA { | digraph NFA { | ||
| Line 16: | Line 16: | ||
""-> q1; | ""-> q1; | ||
| − | q1-> | + | q1->q1 [label="a"]; |
q1->q2 [label="a"]; | q1->q2 [label="a"]; | ||
q2 -> q2 [label="b"]; | q2 -> q2 [label="b"]; | ||
} | } | ||
</graphviz> | </graphviz> | ||
| + | |||
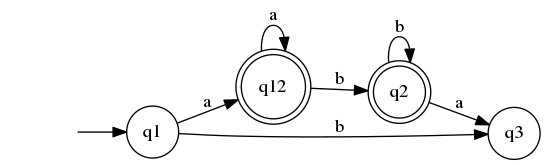
| + | ===DFA=== | ||
<graphviz caption='DFA'> | <graphviz caption='DFA'> | ||
digraph DFA { | digraph DFA { | ||
A: I would say 1 because the $n$ states can be connected through $ε$ moves and hence all of these will be combines to a single start state in DFA.
A: In the worst case this can remain $2^n$ - that is no minimization can be possible. We can see this in the following example
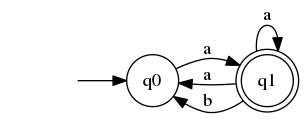
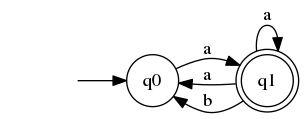
A: I would say 1 because the $n$ states can be connected through $ε$ moves and hence all of these will be combines to a single start state in DFA.
In the worst case this can remain $2^n$ - that is no minimization can be possible. We can see this in the following example